5.1 基本概念

1. 图

图（Graph）是由节点和边组成的，如图5.1和图5.2所示，图中的节点常称为顶点。

图中的顶点表示具有相同特征的数据元素，是对现实世界事物的一种抽象。所有的顶点组成了一个顶点的集合，记作 ​ V ，一般不为空。图中的边表示顶点（数据元素）之间的关系，如果两个顶点具有相邻关系，则在这两个顶点之间就存在一条边。所有的边组成了一个边的集合，记作 ​ E 。一个图 ​ G 可以定义为 ​ G = (V, E) 。

2. 有向图和弧

在图5.1中，​ G_1 是一个有向图，即图中的每条边都有方向。在有向图中，若从顶点 ​ v_i 到顶点 ​ v_j 有一条直接连线，则称顶点 ​ v_i 到顶点 ​ v_j 有一条弧，记作 ​ \langle v_i, v_j \rangle 。其中，弧的始点 ​ v_i 称为弧尾，在图中是不带箭头的一端；弧的终点 ​ v_j 称为弧头，在图中是带箭头的一端。有向图 ​ G_1 表示如下：

​ G_1 = (V, E) ，

其中 ​ V = \{ v_1, v_2, v_3, v_4, v_5 \} ，

​ E = \{ \langle v_1, v_2 \rangle, \langle v_1, v_5 \rangle, \langle v_2, v_3 \rangle, \langle v_3, v_4 \rangle, \langle v_3, v_5 \rangle, \langle v_4, v_1 \rangle, \langle v_4, v_2 \rangle \} 。

3. 有向完全图

对于一个有向图，如果图中任意两个顶点之间都有方向互为相反的两条弧相连接，那么称这样的有向图为有向完全图。在一个包含 ​ n 个顶点的有向完全图中，共有 ​ n(n-1) 条弧。

4. 无向图和边

在图5.2中，​ G_2 是一个无向图，即图中的每条边都没有方向。在无向图中，若从顶点 ​ v_i 到顶点 ​ v_j 有一条直接连线，则称这条连线为这两个顶点之间的一条边，记作 ​ (v_i, v_j) ，表示顶点 ​ v_i 和顶点 ​ v_j 互为邻接点。无向图 ​ G_2 表示如下：

​ G_2 = (V, E) ，

其中 ​ V = \{ v_1, v_2, v_3, v_4, v_5, v_6 \} ，

​ E = \{ (v_1, v_2), (v_1, v_3), (v_1, v_4), (v_2, v_4), (v_3, v_5), (v_3, v_6), (v_5, v_6) \} 。

5. 无向完全图

对于一个无向图，如果图中任意两个顶点都有一条直接边相连接，那么称这样的无向图为无向完全图。可以证明，在一个包含 ​ n 个顶点的无向完全图中，共有 ​ \frac{n(n-1)}{2} 条边。

6. 顶点的度

对无向图而言，顶点的度指的是依附于该顶点的边的个数，即与该顶点相邻接的顶点个数。

例如，在无向图 ​ G_2 中，顶点 ​ v_1 的度为 3，顶点 ​ v_5 的度为 2。对有向图而言，顶点的度为其出度和入度之和，其中出度定义为以该顶点为弧尾的弧的个数，入度定义为以该顶点为弧头的弧的个数。例如，在有向图 ​ G_1 中，顶点 ​ v_1 的度为 3，其中出度为 2，入度为 1；顶点 ​ v_5 的度为 2，其中出度为 0，入度为 2。

7. 权和网

在图中，与边有关联的数据信息称为权值。在实际应用中，权值都是有一定意义的数值。

例如，可以用图表示旅游交通信息，其中描述城市之间距离的数值就是图中边上的权值。边上带权的图称为网，根据图是无向图还是有向图，带权的图又可以分为无向网和有向网。

8. 路径和回路

在有向图中，如果存在顶点序列 ​ \{ v_0, v_1, \ldots, v_k \} ，从顶点 ​ v_0 到顶点 ​ v_k 之间都有弧存在，即 ​ \langle v_0, v_1 \rangle, \langle v_1, v_2 \rangle, \ldots, \langle v_{k-1}, v_k \rangle 分别是图中的弧，那么这个顶点序列 ​ \{ v_0, v_1, \ldots, v_k \} 为从顶点 ​ v_0 到顶点 ​ v_k 的一条有向路径，该序列路径中弧的数目称为路径长度。在无向图中，如果存在顶点序列 ​ \{ v_0, v_1, \ldots, v_k \} ，从顶点 ​ v_0 到顶点 ​ v_k 之间都有边存在，即 ​ (v_0, v_1), (v_1, v_2), \ldots, (v_{k-1}, v_k) 分别是图中的边，那么这个顶点序列 ​ \{ v_0, v_1, \ldots, v_k \} 为从顶点 ​ v_0 到顶点 ​ v_k 的一条无向路径，路径长度为 ​ k 。

若路径中的顶点都不相同，即顶点不重复出现，称这种路径为简单路径。如果 ​ v_0 和 ​ v_k 是同一个顶点，则表示该路径是一条从某个顶点出发又回到自身的路径，称这种路径为回路或环。在回路中，如果除了第一个顶点与最后一个顶点之外，其他的顶点不重复出现，称这种回路为简单回路，或者简单环。例如，在有向图 ​ G_1 中，顶点序列 ​ \{ v_1, v_2, v_3, v_5 \} 是一条路径长度为 3 的简单路径，顶点序列 ​ \{ v_1, v_2, v_3, v_4, v_1 \} 是一条长度为 4 的简单回路。在无向图 ​ G_2 中，顶点序列 ​ \{ v_1, v_3, v_5, v_6 \} 是一条长度为 3 的无向路径，顶点序列 ​ \{ v_1, v_2, v_4, v_1 \} 是一条长度为 3 的简单回路。

9. 子图

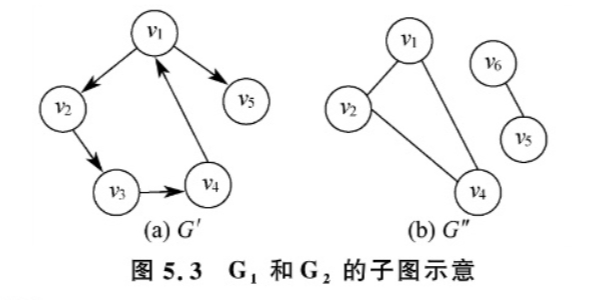
假设有两个图 ​ G = (V, E) 和 ​ G' = (V', E') ，若 ​ V' 是 ​ V 的子集，​ E' 是 ​ E 的子集，则称图 ​ G' 是 ​ G 的一个子图。图5.3示出了 ​ G_1 和 ​ G_2 的子图 ​ G' 和 ​ G'' 。

10. 连通图和连通分量

在无向图中，如果从一个顶点 ​ v_i 到另一个顶点 ​ v_j （​ i \neq j ）之间有一条无向路径，则称顶点 ​ v_i 和 ​ v_j 是连通的。如果任意的两个顶点之间都是连通的，则称该无向图为连通图；否则称为非连通图。非连通图中的每个极大连通子图称为该无向图的连通分量。例如，图5.3(b)中有两个连通分量，如图5.4所示。

11. 强连通图和强连通分量

在有向图中，若图中任意一对顶点 ​ v_i 和 ​ v_j （​ i \neq j ）之间均有从顶点 ​ v_i 到顶点 ​ v_j 的一条有向路径，也有从 ​ v_j 到 ​ v_i 的一条有向路径，则称该有向图是强连通图；否则称为非强连通图。非强连通的有向图的极大强连通子图称为该有向图的强连通分量。例如，图5.3(a)中有两个强连通分量，分别是 ​ \{ v_1, v_2, v_3, v_4 \} 和 ​ \{ v_5 \} ，如图5.5所示。

12. 生成树

假设连通图 ​ G 中有 ​ n 个顶点，则连通图 ​ G 的生成树是该图的一个极小连通子图，它必定包含且仅包含 ​ G 的 ​ n-1 条边。例如，图5.6所示为无向图 ​ G_2 的一棵生成树。
如果在生成树中添加任意一条属于原无向图的边，则必定会产生回路，因为新添加的边使其所依附的两个顶点之间有了第二条路径。如果在生成树中减少任意一条边，则该生成树必然成为非连通的。

13. 生成森林

对于非连通图，对其每个连通分量都可以得到一个极小连通子图，即一棵生成树。由非连通图的所有连通分量的生成树组成的森林，就称为该非连通图的生成森林。