5.6.2 普里姆（Prim）算法

1. 算法思想

普里姆算法从另一个角度来构造无向连通网的最小生成树。其基本思想是：假设无向网表示为 ​ G=(V,E) ，​ V 为网中所有顶点的集合，​ E 为网中所有带权的边集合。最小生成树中的顶点集合用 ​ U 表示，最小生成树中顶点之间的边集用 ​ T 表示，​ U 和 ​ T 初始均为空集。首先在网中任选一个顶点 ​ u 作为最小生成树的根节点，无向网中的顶点分为两类，一类是属于生成树的顶点集，表示为 ​ U = \{u\} ，另一类是不属于生成树的顶点集为 ​ (V - U) 。然后在 ​ (V - U) 中选择顶点 ​ v 加入最小生成树顶点集 ​ U 中，​ v 应满足：​ v 与 ​ U 中的顶点通过边相邻接，且该边上的权值是在连接这两类顶点的所有边中权值最小的，该边即是最小生成树两个节点之间的分支，把它加入最小生成树的边集 ​ T 中。重复上述过程，直到 ​U = V ，即最小生成树中包含了无向网中的所有顶点，由 ​U 中的顶点和 ​ T 中的边就构成了无向网的最小生成树。

2. 算法举例

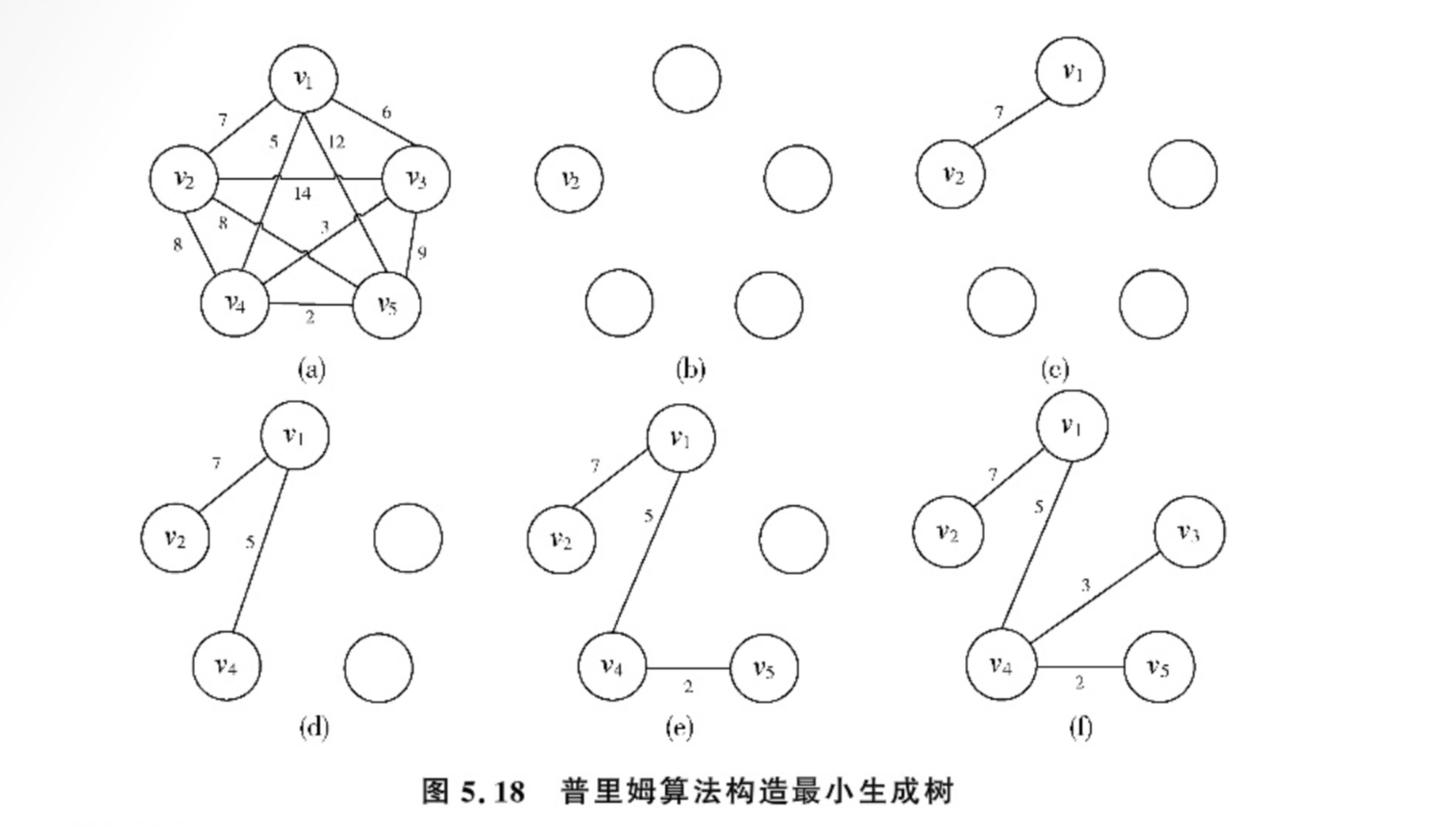
以图 5.18 (a) 所示的无向网为例（与图 5.17 (a) 相同），采用普里姆算法构造它的最小生成树，过程如图 5.18 (b) 至图 5.18 (f) 所示。假设首先选择顶点 ​ v_2 作为最小生成树的根，此时只有顶点 ​ v_2 在生成树中（如图 5.18 (b)）。其余顶点 ​ v_1 、​ v_3 、​ v_4 和 ​ v_5 均不在生成树上，连接这两类顶点的边有 ​ (v_2, v_1) 、​ (v_2, v_3) 、​ (v_2, v_5) 和 ​ (v_2, v_4) ，其中边 ​ (v_2, v_1) 权值最小，选择该边将顶点 ​ v_1 加入生成树（如图 5.18 (c)）。之后连接 ​ \{v_1, v_2\} 和 ​ \{v_3, v_4, v_5\} 两个顶点集的边，除了 ​ (v_2, v_3) 、​ (v_2, v_5) 和 ​ (v_2, v_4) ，又增加了 ​ (v_1, v_3) 、​ (v_1, v_5) 和 ​ (v_1, v_4) ，这六条边中权值最小的边为 ​ (v_1, v_4) ，选该边将顶点 ​ v_4 加入生成树（如图 5.18 (d)）。之后在连接顶点集 ​ \{v_1, v_2, v_4\} 和 ​ \{v_3, v_5\} 的边集 ​ \{(v_1, v_3), (v_1, v_5), (v_2, v_3), (v_2, v_5), (v_4, v_3), (v_4, v_5)\} 中选择权值最小的边 ​ (v_4, v_5) ，依次类推，直到所有顶点加入最小生成树（如图 5.18 (e) 和图 5.18 (f)）。

#include<bits/stdc++.h>
using namespace std;
int g[101][101];//链接矩阵 左边横坐标表示起点，上边纵坐标表示终点。
//对应数组元素的值表示起点到终点的费用
int lowcost[101];//lowcost[j]表示的是节点到U集合的最短距离
// lowcost[j] == 0表示在U集合内， lowcost[j] ！= 0表示在V-U集合内
int closest[101];// (j，closest[j])是顶点j的最小边，权值为lowcost[j]
const int INF=999999;//无穷大
int n;
int sum;//保存最小生成树的权值之和
int prim(int v)
{
    int minv;
    int i,j,k;
    sum=0;
    for(i=1;i<=n;i++)//初始化
    {
        lowcost[i]=g[v][i];//初始时lowcost[i]是起点v到i的边上的权值
        closest[i]=v;//因为初始时U里就是一个v所以v是其余V-U集合中所有节点的最近关系者
    }
    for(i=1;i<n;i++)//循环n-1次，把除了起点v的其余n-1个节点 加入U集合中，就大功告成
    {
        minv=INF;
        for(j=1;j<=n;j++)//遍历不在U集合中的节点（也就是V-U集合中的节点）
        {
            if(lowcost[j]!=0 && lowcost[j]<minv)//通过 lowcost[j]!=0控制在哪个集合
            {
                k=j;//女朋友算法 k保存的是本轮遍历到目前的j到U集合的最短距离
                minv=lowcost[j];//
            }
        }


        sum+=minv;//本轮加入的边的权值就是min 也就是 lowcost[k]
        lowcost[k]=0;//选出的k加入U集合了 就代表 距离为0了，所以lowcost[k]变为0


        for(j=1;j<=n;j++)//选出来的k加入了U集合，就要交投名状
        {//遍历 lowcost[j] 看原来每个V-U中的节点到U集合的距离，比k到 每个V-U中的节点的距离远
            if(lowcost[j]!=0 && g[k][j]<lowcost[j])//那么就更新成k到 每个V-U中的节点的距离
            {
                lowcost[j]=g[k][j];//距离更新
                closest[j]=k;//最近的关系人更新
            }
        }
    }
    return 0;
}

int main()
{
    int i,j;
    cin>>n;
    for(i=1;i<=n;i++)//直接输入方案，也就是直接给二维数组
    {
        for(j=1;j<=n;j++)
        {
            cin>>g[i][j];
        }
    }
    prim(1);
    cout<<sum;
    return 0;
}

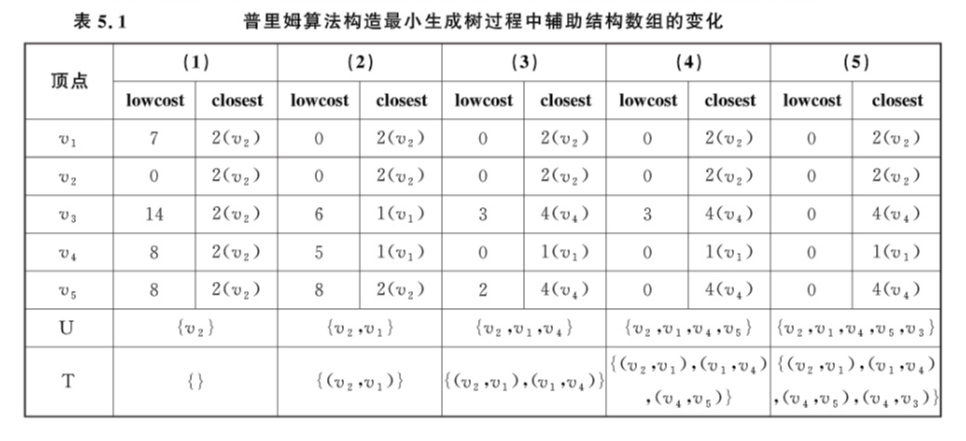
为实现普里姆算法需设置两个辅助数组 ​ lowcost 和 ​ closest ，保存当前时刻从集合 ​ U 到集合 ​ V - U 中每个顶点的权值最小边。​ lowcost[j] 表示节点 ​ j 到 ​ U 集合的最短距离，​ lowcost[j] == 0 表示在 ​ U 集合内，​ lowcost[j] != 0 表示在 ​ V - U 集合内。​ closest 保存该权值最小边在 ​ U 上的顶点，​ (j, closest[j]) 是顶点 ​ j 的最小边，权值为 ​ lowcost[j] 。

算法首先对 ​ lowcost 数组和 ​ closest 数组初始化。接着循环 ​ n - 1 次，将除起点外的其余 ​ n - 1 个顶点加入 ​ U 集合。遍历不在 ​ U 集合的节点，找出当前阶段距离 ​ U 集合最近的顶点 ​ k ，加入 ​ U 集合，同时将 ​ lowcost[k] （即 ​ minv ）累加到 ​ sumv 。然后再次遍历不在 ​ U 集合的顶点，若上一阶段 ​ V - U 的顶点到 ​ U 集的最短距离大于当前阶段 ​ k 加入 ​ U 后这些点到 ​ k 的距离，则更新该顶点到 ​ U 集的最短距离为到 ​ k 的距离。

表 5.1 给出了用上述算法构造网图 5.18 (a) 的最小生成树过程中，​ closest 和 ​ lowcost 以及集合 ​ U 和 ​ T 的变化情况，可加深对普里姆算法的理解。

普里姆算法的时间复杂度为 ​ O(n^2) ，​ n 为顶点数，适用于稠密图。其思想是局部最优（贪心算法思想）加以调整达到全局最优。