《拓扑排序：判断 AOV 网中是否存在有向环及拓扑有序序列的生成》

5.8.2 拓扑排序

AOV 网中不允许出现有向环，如果出现有向环，就意味着某项活动的开始以本身的完成为先决条件，这显然不合理，说明工程设计存在问题。为保证工程顺利完成，必须确保 AOV 网中无有向环。

判断有向网中是否存在有向环的一个方法是对该 AOV 网进行拓扑排序，即构造一个包含网中所有顶点的拓扑有序序列。该序列特点如下：若 AOV 网中存在从顶点 ​ v_i 到顶点 ​ v_j 的弧，则在拓扑有序序列中 ​ v_i 必须在 ​ v_j 前面；若 ​ v_i 和 ​ v_j 之间无弧，则在拓扑有序序列中，这两个顶点的先后次序可任意。

对于图 5.21 描述课程学习先后顺序的 AOV 网，其两个拓扑有序序列为 ​ (c_1, c_2, c_3, c_7, c_4, c_5, c_6, c_8) 和 ​ (c_1, c_2, c_3, c_4, c_5, c_6, c_7, c_8) 。

显然，若 AOV 网中存在有向环，则无法将所有顶点纳入一个拓扑有序序列；反之，若不能从 AOV 网得到拓扑有序序列，则网中必定存在有向环。工程中各项活动的安排，必须按拓扑有序序列的顺序进行才可行。

对 AOV 网进行拓扑排序的方法和步骤：

从 AOV 网中选择一个没有前驱（入度为 0）的顶点并输出；

从 AOV 网中删除该顶点及从它出发的弧；

重复上述两步，直到 AOV 网变空（输出所有顶点）或剩余子图中不存在没有前驱的顶点。

操作结果有两种：一是 AOV 网中全部顶点都被输出，说明网中无有向环；二是网中存在未输出顶点（这些顶点都有前驱），说明网中有有向环。

在拓扑有序序列中出现的第一个顶点，应是在整个 AOV 网中无任何前驱的顶点。输出该顶点后，其在序列中的位置领先于后续输出的顶点，后续拓扑排序过程中无需再考虑该顶点的制约因素，故需删除从该顶点出发的弧。

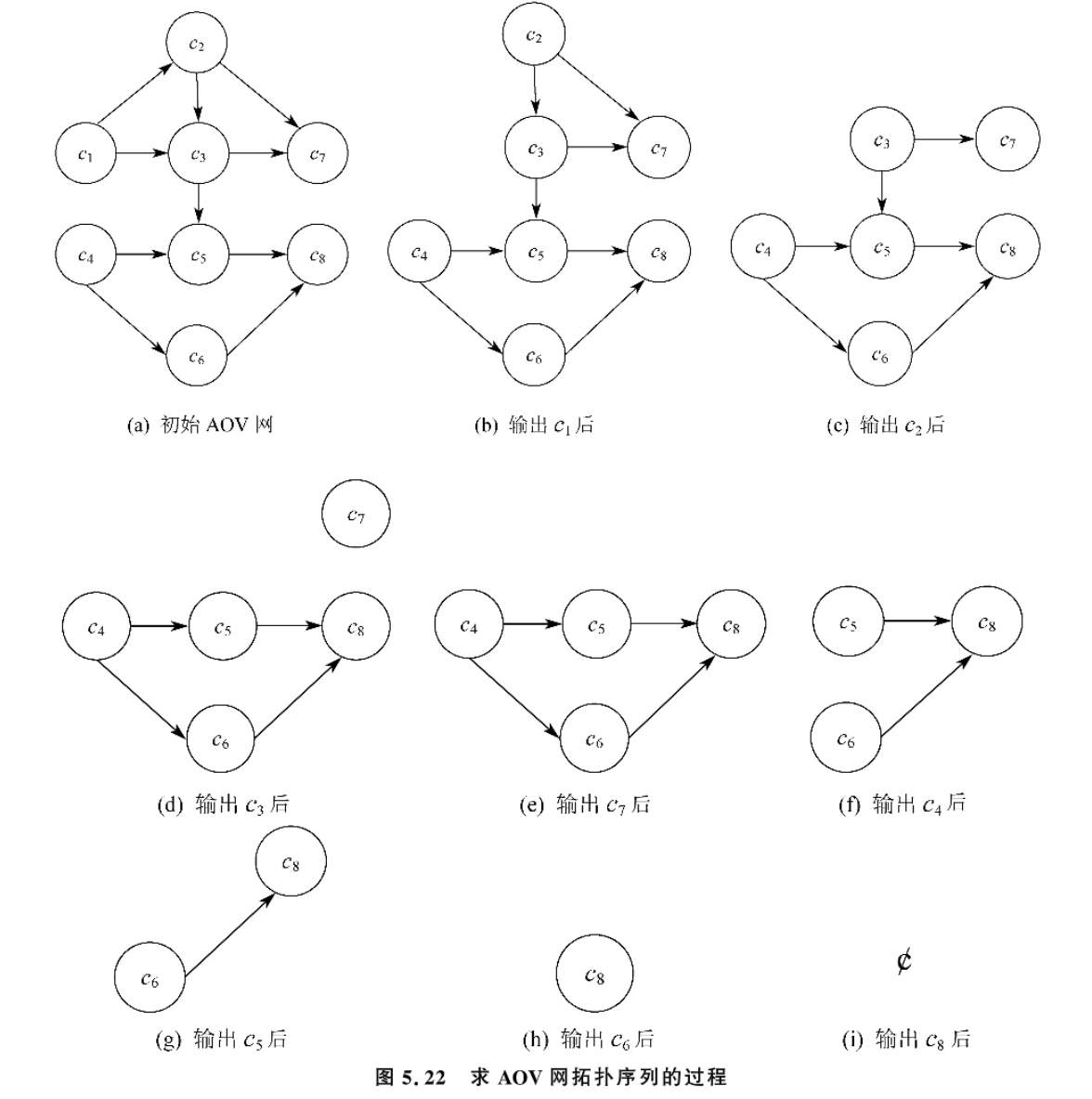
图 5.22 给出对图 5.21 的 AOV 网进行拓扑排序的过程，得到的拓扑排序序列为 ​ c_1, c_2, c_3, c_7, c_4, c_5, c_6, c_8 。

对图 5.22 的 AOV 网采用邻接表存储方式。拓扑排序过程中，每次选择入度为 0 的顶点输出，需用临时数组保存各顶点在算法执行过程中的入度。每输出一个顶点，从 AOV 网中删除该顶点及从它出发的弧（在算法中，删除弧操作不必真正修改图的邻接表结构，只需将保存顶点入度的数组元素值减 1）。为便于处理，算法中可设置队列或栈结构，保存当前入度为零的顶点编号。