5.8 AOV 网与拓扑排序
5.8.1 AOV 网
一个无环的有向图称作有向无环图(Directed Acyclic Graph),简称 DAG 图,它在工程项目的进程管理方面有着广泛而重要的应用。通常一个大的工程可以分成若干个称为 “活动” 的子工程,并且这些子工程之间要满足一定的约束条件,例如某些子工程必须在另一些子工程完成之后才能开始。对整个工程项目,人们关心的是两方面的问题:一是整个工程能否顺利实施;二是完成整个工程项目所需的最短时间。这两个问题也就是有向无环图的拓扑排序和关键路径问题,本节讨论拓扑排序问题,5.9 节将讨论关键路径问题。
一项工程可以包括一些子工程,这些子工程具有相对独立性,通常称这些子工程为 “活动”。子工程之间在进行的时间上存在一定的相互约束关系,例如,软件开发过程中,需求分析阶段必须在系统设计之前进行,系统维护则要在系统实现之后进行。可以使用一个有向图表示这些子工程及其相互约束的关系,如果以有向图中的顶点表示活动,而有向边(弧)表示活动之间的优先关系,那么称这种有向图为活动在顶点上的网络,简称活动顶点网络,或记作 AOV 网(Activity On Vertex Network)。
例如,假设软件学院的学生必须完成一系列专业课程的培训,需要学习表 5.4 所列的各门课程,每个接受培训的学生都必须学完和通过全部的课程才能颁发合格证书。
| 课程编号 | 课程名称 | 先修课程 |
|---|---|---|
| c₁ | 程序设计基础 | 无 |
| c₂ | 离散数学 | c₁ |
| c₃ | 数据结构 | c₁ c₂ |
| c₄ | 计算机组成原理 | 无 |
| c₅ | 操作系统 | c₂ c₄ |
| c₆ | 计算机网络 | c₄ |
| c₇ | 数据库原理 | c₂ c₃ |
| c₈ | Linux 组网 | c₅ c₆ |
整个培训过程就可看作是一项工程,而每门课程的学习就是一项活动,某门课程可能是其他课程的先修课程,而该课程以其他一些课程作为先修课程,各门课程之间的先修关系可以用图 5.21 所示的 AOV 网表示。
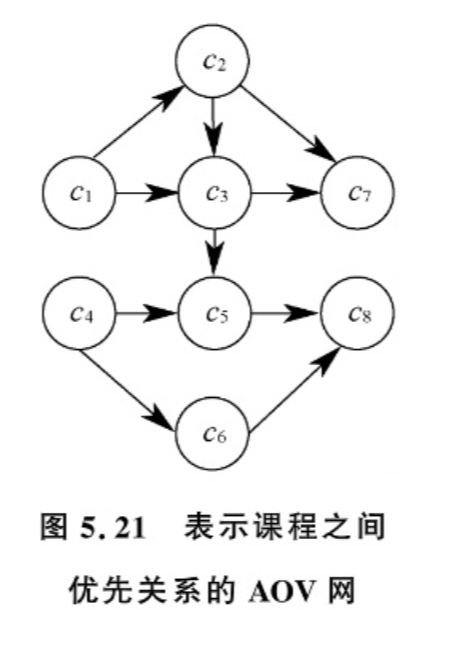
图 5.21 的 AOV 网中,顶点表示课程,弧(有向边)表示课程之间存在的优先顺序关系,若课程 cᵢ为课程 cⱼ的先修课程,则必然存在弧 <cᵢ, cⱼ>。在安排学习顺序时,必须保证在学习某门课程之前,已经学习了其先修课程。
学生必须按照 AOV 网所描述的课程之间的先后顺序进行学习,从图中可以看出,c₁、c₄是独立于其他课程的基础课程,它们没有先修课程;而有的课却需要有先修课程,比如,学习数据结构之前,要先学完程序设计基础和离散数学。
